Мы уже начали разбираться, что такое контекстно--адаптивное двоичное арифметическое кодирование. Сегодня поговорим о том, как двоичный характер закодированной информации изменяет процедуру кодирования и декодирования. Ознакомьтесь с предыдущими главами: часть 1, часть 2.
Входной поток символов должен быть двоичным!
Из самого названия CABAC (cr5GtXLVm5g Adaptive Binary Arithmetic Coding) следует, что в HEVC используется двоичная версия арифметического кодирования, когда алфавит входного сообщения состоит всего из двух символов (0 и 1). Чтобы различать слова, которые обозначают биты выходного потока (результат кодирования), и двоичные символы, представляющие кодируемое сообщение, эти символы называют «бинами». Посмотрим, что изменится, если в представленных на рис. 2–4 блок-схемах учесть двоичный характер кодируемого сообщения.
Прежде всего, необходимо отметить, что из алфавита исчезает символ EOF, обозначающий конец сообщения. Информация об окончании сообщения необходима при декодировании. При отсутствии такой информации декодирование будет продолжаться даже после правильного декодирования всего сообщения. Как в HEVC реализуется передача информации о конце сообщения мы рассмотрим позднее. Здесь же отметим только необходимость реализации процедуры такой передачи.
Что еще поменяется в случае кодирования сообщения, состоящего только из двух символов? Массив P, содержащий кумулятивные вероятности символов, будет содержать теперь только три значения: P={0,PMPS,1}. За PMPS здесь обозначена вероятность появления в сообщении более вероятного символа (если мы из нашего 20-ти символьного сообщения {b, a, b, b, b, b, b, b, b, b, a, b, b, b, b, b, b, b, b, EOF} уберем символ EOF, то длина сообщения станет равна 19/19, а вероятность более вероятного символа «b» будет равна 1819). Т. о. текущий отрезок [L,H) теперь при кодировании будет все время делиться на две части. Длина большей части определяется вероятностью PMPS, меньшей — вероятностью PLPS=1−PMPS. Массив P, по сути дела, выродился в одно число. Этим числом может быть PMPS, но с тем же успехом этим числом может быть и PLPS.
До сих пор положение на числовой оси текущего отрезка, который мы делим при кодировании сообщения, характеризовалось положением конечных точек этого отрезка L и H. Очевидно, что описывать текущее состояние процедуры арифметического кодирования (положение отрезка на числовой оси) можно и с помощью чисел L и R, где R – длина отрезка. Именно такое описание используется в стандарте HEVC.
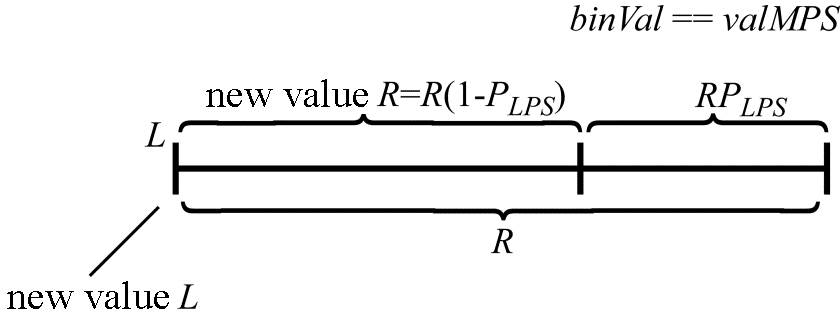
Итак, пусть число, характеризующее соотношение частей отрезка при его итеративном делении, будет равно PLPS. Обозначим, используя обозначения из стандарта HEVC, значение (0 или 1) наиболее вероятного бина в кодируемой последовательности за valMPS. Значение текущего кодируемого бина будем характеризовать величиной binVal. Положение левой границы текущего интервала по-прежнему будем обозначать значением L. Длину текущего интервала – R. В том случае, если значение текущего кодируемого бина равно valMPS, вычисление новых значений L и R по их текущим значениям и PLPSможно вычислить как (рис. 1):
R=R(1−PLPS)=R−R⋅PLPS,
L=L.
Рис. 1. Определение значений L и R при binVal≡valMPS
В том же случае, когда значение кодируемого бина не совпадает со значением valMPS, новые значения L и R определяются выражениями (рис. 2):
R=R⋅PLPS,
L=L+R(1−PLPS).
Рис. 2. Определение значенийL и R при binVal!=valMPS
В результате получаем несколько обновленную блок-схему (рис. 3) алгоритма теперь уже двоичного арифметического кодирования.
Рис. 3. Блок-схема алгоритма процедуры кодирования бина
Процедуру ренормализации при переходе к двоичному кодированию можно было бы и не менять. С другой стороны, небольшие изменения процедуры ренормализации могут несколько упростить алгоритм и снизить вычислительные затраты. В новых терминах L и R процедура ренормализации выполняется циклически до тех пор, пока значение R<1/2. Если при этом L+R<12, то значение закодированного бита определено и равно 0. Если же L>1/2 , то значение закодированного бита равно 1 (упрощенно, детально процедура описана на рис. 2 в части 2 и в пояснениях к нему). Очевидно, что значения закодированных битов будут полностью определены и в том случае, когда R<1/4. Если при этом L<1/4, то текущий отрезок полностью лежит в области [0,1/2] и, таким образом, значение закодированного бита равно 0. В том случае, когда R<1/4 и L⩾1/2, текущий отрезок полностью лежит в области [1/2,1], а значение закодированного бита равно 1. Блок-схема модифицированной процедуры ренормализации при кодировании приведена на рис. 4.
Рис. 4. Блок-схема алгоритма ренормализации при кодировании
Посмотрим теперь, как двоичный характер закодированной информации изменит процедуру декодирования. Процедура арифметического декодирования заключается в этом случае в итеративном делении текущего отрезка на две части, длины которых пропорциональны 1−PLPS и PLPS. При каждом делении производится проверка какому из двух интервалов принадлежит двоичное число, представляющее закодированное сообщение. Этот интервал и становится текущим.
Пусть несколько бит закодированного сообщения содержатся в переменной ivl0ffset (используем здесь обозначение этой переменной из стандарта HEVC). Текущий отрезок по-прежнему будем характеризовать положением на числовой оси его левого конца L и его длиной R. Процедура декодирования иллюстрируется на рис. 5, где представлены две последовательные итерации. В первой из них число ivlOffset (положение числа внутри текущего отрезка отмечено кружком) содержится внутри отрезка [L,L+R(1−PLPS)]. Как следствие, декодированный бин имеет значение valMPS. На второй итерации ivlOffset попадает в меньший из интервалов и декодированный бин имеет значение !valMPS.
Рис. 5. Деление отрезка при декодировании
Из рисунка видно, что выбор отрезка на каждой итерации определяется сравнением значения ivlOffset с правой границей интервала L+R⋅(1−PLPS). В случае, когда ivlOffset попадает в больший отрезок, соответствующий вероятности PMPS, величина R приобретает новое значение R⋅(1−PLPS), а величина L не меняется. В том же случае, когда ivlOffset попадает в меньший отрезок, соответствующий вероятности PLPS, левая граница интервала смещается на точку L+R⋅(1−PLPS), а новое значение R определяется как R⋅PLPS. Заметим также, что во втором случае вместо изменения значения L можно изменить значение величины ivlOffset на значение ivlOffset−R⋅(1−PLPS). Теперь значение ivlOffset характеризует не само двоичное число, представляющее закодированное сообщение, а положение этого числа относительно левой границы текущего интервала. Тогда величина L, сама по себе, перестает использоваться в процедуре декодирования. Для принятия решения о том, какой из двух отрезков на каждой итерации сделать текущим, достаточно сравнить значение ivlOffset с величиной R⋅(1−PLPS). Блок-схема алгоритма декодирования приведена на рис. 6.
Рис. 6. Блок-схема алгоритма декодирования
Изменение смысла величины ivlOffset при двоичном декодировании также существенно меняет (упрощает) и процедуру ренормализации. Процедура ренормализации запускается в том случае, когда длина текущего интервала становится меньше 1/4. Также как и ранее ренормализация удваивает величину R. Однако, теперь вычислять величину L нет необходимости. Т. к. теперь значение ivlOffset – это разница между числом, представляющим закодированное сообщение и левой границей текущего интервала, то при нормализации достаточно безусловно удвоить число ivlOffset, а в освободившийся разряд добавить бит из закодированного сообщения, повышая точность представления ivlOffset. Блок-схема модифицированного алгоритма ренормализации при двоичном декодировании представлена на рис. 7.
Рис. 7. Блок-схема алгоритма ренормализации при декодировании
В представленной блок-схеме используется функция read_bit(), выполняющая очевидное из ее названия действия: эта функция считывает очередной бит из битового потока, представляющего закодированное сообщение. Также в блок-схеме использовано обозначения «|» побитовой операции «или» из языка C.
Об авторе
Олег Пономарев — специалист в области распространения радиоволн, статистической радиофизики, доцент кафедры радиофизики НИ ТГУ, кандидат физико-математических наук. 16 лет занимается вопросами видео кодирования и цифровой обработки сигналов. Руководитель исследовательской лаборатории Elecard.





0 комментариев